UNIDAD DECIMAL

UNIDAD DECIMAL

Youtube: https://www.youtube.com/watch?v=fae6X1jg3nE

¿Qué son los números decimales?

Los números decimales se utilizan para representar números más pequeños que la unidad.

Los números decimales se escriben a la derecha de las Unidades separados por una coma. Es decir:

Centenas   Decenas   Unidades , Décimas   Centésimas   Milésimas

En la imagen que aparece a continuación, el primer cuadrado representa la Unidad. Si esta unidad la dividimos en 10 partes iguales (segundo cuadrado), representaremos las Décimas. Si las décimas las dividimos en 10 partes iguales o la unidad en 100 partes iguales (tercer cuadrado), representaremos las Centésimas.

Veamos algunos ejemplos

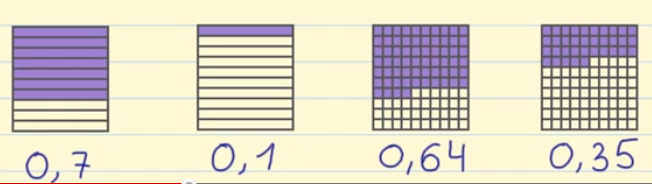
• Primer ejemplo: Si la unidad la dividimos en 10 partes iguales, tendremos décimas. Y hemos coloreado 7 de estas partes. La forma de escribirlo es 0 unidades, 7 décimas = 0,7
• Segundo ejemplo: En el segundo ejemplo también tenemos décimas y tenemos coloreadas 1. Se escribirá de la siguiente forma: 0 unidades, 1 décima = 0,1
• Tercer ejemplo: En el tercer ejemplo tenemos representadas centésimas, de las cuales tenemos coloreadas 6 décimas y 4 centésimas. Por lo tanto se escribirá: 0 unidades, 6 décimas 4 centésimas = 0,64
• Cuarto ejemplo: Tenemos centésimas (la unidad entre 100), de las cuales tenemos coloreadas 3 décimas y 5 centésimas. Lo escribiremos: 0 unidades, 3 décimas 5 centésimas = 0,35

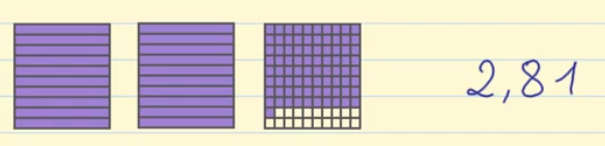
• Quinto ejemplo: Tenemos dos unidades enteras coloreadas y de la tercera unidad, que está dividida en centésimas, tenemos 8 décimas coloreadas y una centésima coloreada. Por lo tanto, se escribirá: 2 unidades, 8 décimas 1 centésimas = 2,81

¿Cual es la relación de los decimales con las fracciones?

• La Unidad se representa por 1
• La Décima es la unidad dividida en 10 partes iguales = 1/10 = 0,1
• La Centésima es la unidad dividida en 100 partes iguales = 1/100 = 0,01
• La Milésima es la unidad dividida en 1000 partes iguales = 1/1000 = 0,001

Ejemplo para pasar de decimal a fracción:

7,508

Nos fijamos en el último número, en el 8, que ocupa el lugar de las milésimas, por lo tanto el denominador tendrá que ser 1000. Y en el numerador escribiremos el número completo sin la coma. 7,508 = 7508/1000

Ejemplo para pasar de fracción a decimal:

402/100

Como el denominador es 100, el último número del numerador (el 2) , tiene que ser las centésimas, el anterior (el 0) tienen que ser las décimas y el anterior a éste (el 4) tiene que ser las unidades, poniendo la coma detrás de las unidades. Por lo tanto, 402/100 = 4,02

Sistema Métrico Decimal

Este sistema fue creado en una convención mundial de ciencia celebrada en París, Francia; en el siglo XVII para ser exactos, allá por el año 1795. Este sistema fue muy importante porque fue el primer patrón que existió para las unidades de medidas, entre ellas se encuentras las unidades como el metro, el kilogramo-peso y el litro. ¿Qué usaron para definir estas unidades?, pues aquí viene lo importante, para definir dichas unidades, utilizaron la dimensión de la tierra y la densidad del agua.

Se dice que para medir las longitudes en ese tiempo, se dividió un meridiano de nuestro planeta en 40 millones de partes iguales, y a cada parte de longitud se le llamó metro.

Después de realizar dicho acuerdo con la longitud, ésta misma sirvió de ejemplo para obtener las demás unidades. Es por eso que la palabra metro significa “medida”.

Una característica importante de éste sistema, fue sin duda la división decimal que tenía; por ejemplo el uso de los prefijos como: deci, centi o mili.

• Decímetro = décima parte del metro
• Centímetro = centésima para del metro
• Milímetro = la milésima parte del metro

Por otra parte tenemos también a los prefijos como: deca, hecto, kilo.

• Decámetro = diez veces el valor del metro
• Hectómetro = cien veces el valor del metro
• Kilómetro = mil veces el valor del metro

CONVERSIÓN DE UNIDADES

Youtube: https://www.youtube.com/watch?v=SkfXl_-vUY8&feature=emb_title

                 https://www.youtube.com/watch?v=Xu0lcWEO9nI

La conversión de unidades es la transformación de una cantidad, expresada en un cierta unidad de medida, en otra equivalente, que puede ser del mismo sistema de unidades o no.

Este proceso suele realizarse con el uso de los factores de conversión y las tablas de conversión.

Frecuentemente basta multiplicar por una fracción (factor de conversión) y el resultado es otra medida equivalente, en la que han cambiado las unidades. Cuando el cambio de unidades implica la transformación de varias unidades se pueden utilizar varios factores de conversión uno tras otro, de forma que el resultado final será la medida equivalente en las unidades que buscamos, por ejemplo si queremos pasar 8 metros a yardas, lo único que tenemos que hacer es multiplicar 8 x (0.914)=7.312 yardas.

Alguna equivalencia 

1 m = 100 cm

1 m = 1000 mm

1 cm = 10 mm

1 km = 1000 m

1 m = 3.28 pies

1 m =  0.914 yardas 

1 pie = 30.48 cm

1 pie = 12 pulgadas 

1 pulgada = 2.54 cm

1 milla = 1.609 km

1 libra = 454 gramos

1 kg = 2.2 libras 

1 litro = 1000 Cm³

^{1 hora = 60 minutos}

^{1 hora = 3600 segundos}

^{Factor de Conversion} 

Un factor de conversión es una operación matemática, para hacer cambios de unidades de la misma magnitud, o para calcular la equivalencia entre los múltiplos y submúltiplos de una determinada unidad de medida.

Dicho con palabras más sencillas, un factor de conversión es "una cuenta" que permite expresar una medida de difentes formas. Ejemplos frecuentes de utilización de los factores de conversión son:

• Cambios monetarios: euros, dólares, pesetas, libras, pesos, escudos...
• Medidas de distancias: kilómetros, metros, millas, leguas, yardas...
• Medidas de tiempo: horas, minutos, segundos, siglos, años, días...
• Cambios en velocidades: kilómetro/hora, nudos, años-luz, metros/segundo..

 ^{un ejemplo de una convercion multiple aqui lo que hizo basicamente fue millas /hora a Pies /seg.} 

^{pero como existe un valor directo de milla a pies tubo que convertir primero las millas a metros para despues poder convertilo a pies y una vez ya teniendo eso poder convertir las hora a segundos} 

  ^{otros ejemplos} 

  Queremos pasar 2 horas a minutos:

 ^{Para convertir esta cantidad lo que hacemos es poner la unidad que queremos eliminar en el denominador y la unidad a la que queremos convertir en el numerador, para asi poder multiplicar el 2 con el numerador que es 60 y asi obtener el valor de 120 minutos} 

Queremos pasar 30 cm a m:

 

Queremos pasar 120 km/h a m/s:

 

Problemas de conversión de medidas de longitud nº 1

El Pirata Barba Plata ha llegado a la isla del Coral para buscar un tesoro. En el mapa pone que, desde la orilla, debe recorrer 3,7 hm a la pata coja hacia el centro de la isla, y después otros 8,5 dam dando volteretas en la misma dirección. ¿Cuántos metros recorrerá en total desde la orilla hasta el tesoro? Expresa el resultado también en kilómetros.

Para responder a la pregunta, debemos sumar las dos distancias. Pero, ¿se pueden sumar hectómetros más decámetros?

¡NO, porque son unidades distintas!

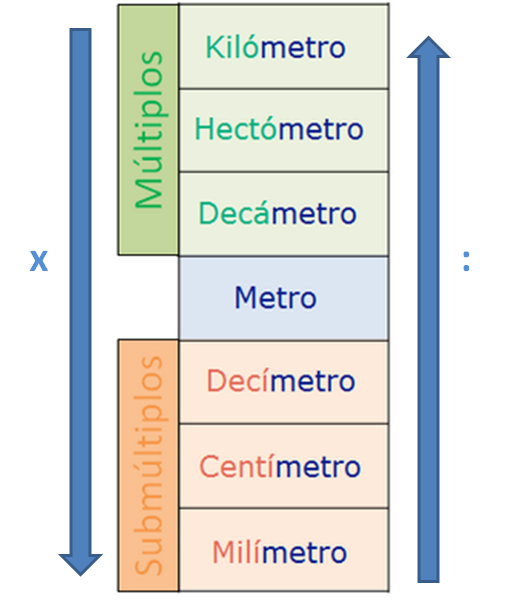
Como nos piden que respondamos en metros, pasaremos ambas distancias a metros. Para ello, nos podemos fijar en esta escala para acordarnos del orden de las distintas unidades.

Fíjate que:

• Cuando el orden es descendente, las unidades se convierten multiplicando
• Cuando el orden es ascendente, las unidades se convierten dividiendo.

Vemos que para pasar de hm y dam a metros, la flecha va hacia abajo, por lo que hay que multiplicar.

Como 1 hm = 100 m… Entonces 3,7 hm = 3,7 x 100 m = 370 m

Como 1 dam= 10 m… Entonces 8,5 dam = 8,5 x 10 = 85 m

Ahora sí podemos sumar:

370 m + 85 m = 455 m

También debemos expresar el resultado en km. Fijándonos en la tabla, vemos que desde los metros a los km la flecha va hacia arriba, por lo que hay que dividir:

Como 1 km = 1000 m… Entonces 455 m = 455:1000 km = 0,455 km

Por lo tanto, la respuesta a este problema es:

455 metros, o, lo que es lo mismo, 0,455 kilómetros

Problemas de conversión de medidas de longitud nº 2

¡Qué pelo más bonito tiene Gabriela! Antes era la chica que más largo tenía el pelo de toda la clase: la melena le medía 6 decímetros de longitud. Pero ayer se lo cortó 25 centímetros, así que ahora la chica con el pelo más largo de la clase es María. ¿Cuántos centímetros mide la melena de Gabriela ahora? Expresa el resultado también en milímetros.

Para saber qué longitud tiene ahora su melena, debemos restar las longitudes, pero lo primero es convertirlas a la misma unidad. La unidad que nos piden es centímetros, así que pasaremos el primer dato a cm. Como de dm a cm hay que bajar, tenemos que multiplicar:

Como 1 dm = 10 cm… Entonces 6 dm = 6 x 10 cm = 60 cm

Ahora restamos:

60 cm – 25 cm = 35 cm

Para expresar la respuesta en mm, también tenemos que bajar, es decir, multiplicar:

Como 1 cm = 10 mm… Entonces 35 cm = 35 x 10 mm = 350 mm

Por lo tanto, la respuesta a este problema es:

35 centímetros, o, lo que es lo mismo, 350 milímetros

Problemas de conversión de medidas de longitud nº 3

Un oso al que le encanta la miel quiere sacar miel de una colmena que hay en la rama de un árbol, pero está demasiado alta. Para alcanzarla, se sube en una roca de 12 dm de alto que hay justo debajo y, con las garras muy estiradas, llega justo a cogerla. Si este oso cuando se estira mide exactamente 2,3 m, ¿a qué distancia del suelo estaba exactamente la colmena?

Como en el primer problema, para resolverlo es necesario sumar las dos distancias. Pero primero debemos convertirlas. Pero en este problema no nos dicen las unidades que debemos utilizar, así que podemos expresar el resultado en la unidad que mejor nos parezca. Elegiremos los metros:

Pasamos los dm a m (como en la escala hay que subir, tendremos que dividir entre 10):

Como 1 m = 10 dm … Entonces 12 dm = 1,2 m

Ahora sumamos:

1,2 + 2,3 = 3,5 m

Por lo tanto, la respuesta a este problema es:

3,5 metros