Profesora Dora Liliana - GIDELPA
PERIMETRO
 Youtube:
https://www.youtube.com/watch?v=-FvTH9sdL3Q
Youtube:
https://www.youtube.com/watch?v=-FvTH9sdL3Q
Profesora Dora Liliana - GIDELPA

El perímetro es uno de los conceptos bases de la geometría, cuando nos referimos a figuras planas. Calcular el perímetro de cualquier forma geométrica plana es bastante sencillo, si conoces la fórmula.
Podríamos decir que el perímetro es la frontera de la figura geométrica; mientras que el área es la medida de su superficie interior.
Calcular perímetro de los polígonos
Los polígonos son figuras geométricas planas compuestas por una secuencia finita de segmentos rectos consecutivos que encierran una región en el plano. Estos segmentos son llamados lados. El perímetro de un polígono es la suma de las longitudes de todos sus lados. Vamos a ver en particular los polígonos más simples: cuadrado, rectángulo y triángulo.
Perímetro de un cuadrado
No hay nada más fácil que calcular el perímetro del cuadrado. Sabemos que un cuadrado tiene cuatro lados iguales, por lo tanto es tan sencillo como multiplicar por 4 la longitud de uno de sus lados:
Ejemplo
Vamos a calcular el perímetro (P) de un cuadrado de 6 cm de lado:
P = 4 . 6
P = 24 cm
ATENCIÓN 👉 Esta fórmula también es válida para el rombo, porque tiene los cuatro lados iguales.
Perímetro de un rectángulo
Para calcular el perímetro del rectángulo tenemos que recordar que tiene dos pares de lados iguales, por lo tanto vamos a sumar la longitud de dos lados diferentes (la altura y la base), y multiplicar el resultado por 2:
Ejemplo
Tenemos un rectángulo de 7 cm de base por 5 de altura:
P = 2 . (7+5)
P = 2 . 12
P = 24 cm
ATENCIÓN 👉 Esta fórmula también es válida para el romboide (paralelogramo que tiene lados contiguos desiguales y no tiene ángulos rectos)
Perímetro de un triángulo
Para calcular el perímetro del triángulo tenemos que saber qué tipo de triángulo es: equilátero, escaleno o isósceles.
Triángulo equilátero
Tiene sus tres lados iguales, por lo que solo tenemos que multiplicar la longitud de un lado por 3:
Ejemplo
Tenemos un triángulo equilátero de 7 cm de lado:
P = 3 . 7
P = 21 cm
Triángulo isósceles
El isósceles tiene dos lados de igual longitud, mientras que el tercero es diferente. Por lo tanto tenemos que multiplicar la longitud de uno de los lados iguales por 2, y sumarle la longitud del lado desigual:
Ejemplo
Tenemos un triángulo isósceles con dos lados de 10 cm y un lado de 6 cm:
P = 2 . 10 + 6
P = 20 + 6
P = 26 cm
Triángulo escaleno
El triángulo escaleno es el que tiene los tres lados diferentes. Así que solo tendremos que sumarlos:
Ejemplo
Tenemos un triángulo cuyos lados miden 5, 7 y 8 cm:
P = a + b + c
P = 5 + 7 + 8
P = 20 cm
Perímetro de una circunferencia
La circunferencia es la línea curva cerrada que delimita al círculo. Por lo tanto el perímetro de un círculo es igual a la longitud de su circunferencia.
Tenemos dos fórmulas posibles para calcularlo:
- Multiplicando PI (π) por el diámetro (d): P =π x d
- Multiplicando dos veces PI (π) por el radio (r): P = 2π x r
RECUERDA 👉 El número PI, cuyo símbolo es π, es la relación entre la longitud de una circunferencia y su diámetro. Es decir, las veces que el diámetro entra en la circunferencia. Es un número constante, porque no importa cuál sea la circunferencia del círculo, el número π será siempre el mismo. Tiene un número indefinido de decimales (actualmente se han calculado dos billones y medio), pero para realizar cálculos matemáticos se utilizan cuatro: π = 3.1416
Ejemplo
Si tenemos un círculo de 5 cm de diámetro, y por lo tanto de 2,5 cm de radio, el resultado es el siguiente usando la primera fórmula:
P =π x d
P = 3.1416 x 5
P = 15,708 cm
Si usamos la segunda fórmula:
P = 2π x r
P = 2(3.1416) x 2.5
P = 6.2832 x 2.5
P = 15,708 cm
PLANO CARTESIANO
EL PLANO CARTESIANO.
El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.
El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados. Las coordenadas se forman asociando un valor del eje de las "X" y uno de las "Y", respectivamente, esto indica que un punto se puede ubicar en el plano cartesiano con base en sus coordenadas, lo cual se representa como:
P (x, y)
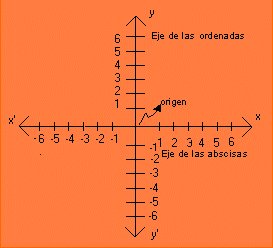
Para localizar puntos en el plano cartesiano se debe llevar a cabo el siguiente procedimiento:
1. Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas o hacia a izquierda si son negativas, a partir del punto de origen, en este caso el cero.
2. Desde donde se localiza el valor de x, se cuentan las unidades correspondientes hacia arriba si son positivas o hacia abajo, si son negativas y de esta forma se localiza cualquier punto dadas sus coordenadas.

Ejemplos:
Localizar el punto A ( -4, 5 ) en el plano cartesiano. Este procedimiento también se emplea cuando se requiere determinar las coordenadas de cualquier punto que esté en el plano cartesiano.
Determinar las coordenadas del punto M.
Las coordenadas del punto M son (3,-5).

De lo anterior se concluye que:
Para determinar las coordenadas de un punto o localizarlo en el plano cartesiano, se encuentran unidades correspondientes en el eje de las x hacia la derecha o hacia la izquierda y luego las unidades del eje de las y hacia arriba o hacia abajo, según sean positivas o negativas, respectivamente.
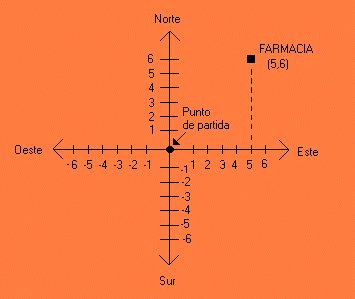
Doña Lupe nos ha dicho que su farmacia está dentro del centro de la ciudad . Supongamos que deseamos saber la ubicación exacta de la farmacia de Doña Lupe. Una vez que ya estamos en el centro le preguntamos a un policía para que nos oriente. El policía nos ha dicho que caminemos 5 cuadras hacía el este y 6 cuadras hacía el norte para llegar a la farmacia.La cantidad de cuadras que tenemos que caminar las podemos entender como coordenadas en un plano cartesiano.
Lo anterior lo podemos expresar en un plano cartesiano de la siguiente manera:
Para el problema planteado , el origen del plano será el punto de partida que es en donde le preguntamos al policía sobre la ubicación de la farmacia.
Funciones lineales:
Esta clase de funciones tienen dos características esenciales:
- Las variaciones entre dos valores de la variable independiente y la de sus correspondientes de la variable dependiente son uniformes.
- Todos los puntos de su gráfica están alineados.
Funciones de proporcionalidad directa:
Si en todos los pares de valores de una función de proporcionalidad directa dividimos la ordenada por la abscisa, obtenemos siempre el mismo número. Ese valor se llama constante de proporcionalidad, y se escribe habitualmente k.
Funciones de proporcionalidad inversa:
Si en todos los pares de valores de una función de proporcionalidad inversa multiplicamos la ordenada por la abscisa, obtenemos siempre el mismo número, que es la constante de proporcionalidad, y habitualmente se escribe k.
ACTIVIDAD
Realiza lo siguiente,
1) En tu cuaderno, realiza un esquema de un plano cartesiano con sus puntos X y Y
2) Localiza los siguientes pares ordenados en el plano:
- A (2,3)
- B (-3,4)
- C) (3,2)
- D (3,0)






Profe tengo una pregunta hay que copiar todo lobque aparaece hay¿en un dia?
ResponderBorrarNo soy la profesora pero , no necesariamente lo tienes que copiar en un día yo llevo 2 y ya voy a acabar
BorrarYo tampoco soy la profe pero yo en media tarde termine lo que es El perimetro
ResponderBorrarProfesora Soy Maicol Madrid Apenas Copiemos Le Mandamos Foto?
BorrarProfe acabamos y oe mandamos las fotos y ya
ResponderBorrar