TRIANGULOS

EL TRIANGULO

El triángulo es un polígono de tres lados que da origen a tres vértices y tres ángulos internos. Es la figura más simple, después de la recta en la geometría. Como norma general un triángulo se representa con tres letras mayúsculas de los vértices (ABC). Los triángulos son las figuras geométricas más importantes, ya que cualquier polígono con un número mayor de lados puede reducirse a una sucesión de triángulos, trazando todas las diagonales a partir de un vértice, o uniendo todos sus vértices con un punto interior del polígono.

Es importante destacar que de entre todos los triángulos sobresale el triángulo rectángulo cuyos lados satisfacen la relación métrica conocida como teorema de pitagora.

Herón de Alejandría fué un ingeniero y matemático griego que vivió durante el siglo I aC, éste escribió una obra llamada La Métrica, donde se dedicó al estudio de los volúmenes y áreas de distintas superficies y cuerpos. Pero sin duda lo más importantes realizado por éste matemático fue la conocida Fórmula de Herón, ésta se encarga de relacionar directamente la zona de un triángulo con las longitudes de sus lados.

Un triángulo rectángulo consiste en un ángulo de 90° y dos ángulos agudos. Cada ángulo agudo de un triángulo rectángulo tiene las funciones de seno, coseno y tangente. Éstas a su vez, son puntos ubicados en dos de las tres patas de un triángulo rectángulo.

El seno de un ángulo es la relación entre la longitud de la pierna opuesta del ángulo dividida por la longitud de la hipotenusa.

El coseno de un ángulo es la relación entre la longitud de la pierna adyacente al ángulo dividido por la longitud de la hipotenusa.

La tangente de un ángulo es la relación entre la longitud de la pierna opuesta del ángulo dividida por la longitud del lado adyacente del ángulo.

Elementos De Los Triángulos

Como figura geométrica más sencilla, los triángulos han sido analizados con un alto grado de detalle desde las civilizaciones antiguas. Los filósofos griegos ofrecieron descripciones muy minuciosas de sus formas y sus elementos, con sus propiedades y sus relaciones genuinas.

Familias de triángulos

Se llama triángulo a un polígono de tres lados. Por tanto, el triángulo es la figura geométrica cerrada más simple que existe, y se distingue por poseer tres ángulos interiores y carecer de diagonales. La confluencia o intersección entre cada dos lados del triángulo se llama vértice.

Se han propuesto varias clasificaciones para los triángulos:

Según la longitud de sus lados, se distingue entre triángulos equiláteros, con los tres lados iguales; isósceles, con dos lados iguales y uno desigual, y escalenos, con los tres lados distintos.
Atendiendo a sus ángulos interiores, pueden ser acutángulos, cuando los tres ángulos son agudos; rectángulos, si poseen un ángulo recto (90º), y obtusángulos, cuando alguno de los ángulos es obtuso (mayor de 90º).

Los triángulos rectángulos constituyen una familia geométrica de especial interés, ya que sirven de base para la definición de las razones y las funciones trigonométricas. En los triángulos rectángulos, se llama hipotenusa al lado opuesto al ángulo recto, y catetos a los otros dos lados.

Clases de triángulos.

Propiedades de los triángulos

Todo triángulo verifica un conjunto de propiedades geométricas esenciales muy interesantes:

Cualquiera de sus lados es menor que la suma de los otros dos y mayor que su diferencia.
Los tres ángulos interiores de un triángulo suman siempre un ángulo llano (180º). Por tanto, los triángulos equiláteros tienen tres lados iguales y tres ángulos iguales, de un valor de 60º.
El ángulo mayor se opone al lado más largo del triángulo, y al contrario. Asimismo, si dos lados son iguales, sus ángulos interiores opuestos son también iguales, y viceversa. Así, por ejemplo, los triángulos equiláteros son regulares.

Elementos de un triángulo

Además de los lados y los ángulos interiores, en un triángulo pueden definirse otros elementos de interés desde el punto de vista de la geometría.

Se llama altura a cada una de las perpendiculares trazadas desde un lado al vértice opuesto. Las tres alturas de un triángulo se cortan en un punto denominado ortocentro.
Las mediatrices de un triángulo son cada una de las perpendiculares de sus lados desde su punto medio. La intersección de las tres mediatrices de un triángulo se conoce por circuncentro (que es, además, el centro de la circunferencia circunscrita al triángulo).
Se denomina mediana de un triángulo a cada una de las rectas trazadas desde el punto medio de un lado al vértice opuesto. Las tres medianas de un triángulo se cortan en un punto llamado baricentro o, también, centro de gravedad del triángulo.
Las bisectrices son las rectas que dividen por la mitad cada uno de los ángulos del triángulo. Las tres bisectrices de un triángulo intersecan en un punto denominado incentro (que coincide con el centro de la circunferencia inscrita en el triángulo).

Triangulaciones

Una de las razones que explica el interés de la figura del triángulo en geometría es posibilidad de describir cualquier polígono convexo como una combinación de triángulos. Esta técnica, llamada triangulación, permite establecer relaciones entre los elementos de los polígonos, así como facilitar el cálculo de sus áreas y otras propiedades geométricas.

Para triangular un polígono convexo, basta con elegir uno de sus vértices y trazar desde él todas las diagonales a los vértices opuestos. Otro procedimiento válido de triangulación consiste en fijar uno o varios puntos interiores del polígono y unirlos mediante rectas con cada uno de los vértices.

Ejemplos de triangulaciones posibles de un mismo pentágono.

En los polígonos convexos se cumple una propiedad general: la suma de los ángulos interiores del polígono es siempre igual a tantos ángulos llanos (180º) como lados tiene el polígono menos 2.

Ilustración de la propiedad de los ángulos interiores de un polígono.

Triángulos según la longitud de sus lados

De acuerdo a la longitud de sus lados, un triángulo pueden clasificarse en equilátero, donde los tres lados del triángulo son iguales; en isósceles, el triángulo tiene dos lados iguales y uno desigual, y en escaleno, donde el triángulo tiene los tres lados desiguales.

Triángulo Equilátero

Este tipo de triángulo tiene los tres lados iguales, es decir, tienen la misma longitud. Este tipo de triángulo es muy usado en la práctica, debido a que sus propiedades son simétricas y de fácil uso.

Triángulo Escaleno

Este triángulo tiene sus tres lados distintos entre sí, es decir, las longitudes de sus lados son diferentes, no tienen ningun lado común.

Triángulo Isósceles

Es el triángulo que tienen sus dos lados iguales, el tercer lado recibe el nombre de base. Los ángulos en esta base son iguales recíprocamente, si dos ángulos de un triángulo son iguales, los lados opuestos a dichos ángulos también serán iguales.

Triángulos según sus ángulos

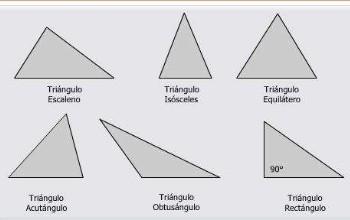
También se pueden clasificar según la medida de sus ángulos, éstos puede ser:

Triángulo Rectángulo

Si un triángulo presenta un ángulo recto o ángulo de 90° se dice que es rectángulo. Otra característica es que en el triángulo rectángulo, los lados que forman el ángulo recto se llaman catetos y el lado opuesto se llama hipotenusa.

Triángulo Obtusángulo

Es el triángulo que presenta a uno de los tres ángulos como obtuso; es decir, un ángulo mayor que 90°.

Triángulo Acutángulo

Es el triángulo donde los tres ángulos son agudos; es decir, ángulos menores que 90°.

Triángulo Equiángulo

Estos triángulos también son llamados equiláteros, sus tres lados internos son iguales, con una medida de 60° cada uno y además, sus tres ángulos son congruentes.

Esta imagen de triángulo tiene como característica principal que la suma de sus tres ángulos siempre es igual a 180°. Si conocemos dos de ellos podemos calcular cuánto medirá el tercero.

El área de un triángulo es igual a su base (uno cualquiera de sus lados) por su altura (segmento perpendicular a la base o a su prolongación, trazado desde el vértice opuesto al lado de la base) partido por dos, en otras palabras, es (base x altura)/2.

ÁREA DE UN TRIANGULO

Youtube: https://www.youtube.com/watch?v=QtHQFAbgdPU

https://www.youtube.com/watch?v=OIGrVkJr8u8

https://www.youtube.com/watch?v=4_O4XHvAB8o

El área de un triángulo es igual a base por altura partido por 2.

La altura es la recta perpendicular trazada desde un vértice al lado opuesto (o su prolongación).